Before the vector calculus was invented mathematicians used to do vector calculus like operations using quaternions. Quaternions are four dimensional extension of complex numbers. They have two additional imaginary units $j$ and $k$. Quaternion multiplication is non-commutative and is defined by the formula:

$$i^2=j^2=k^2=ijk=-1$$

One easy way to remember the multiplication rules is with the following diagram:

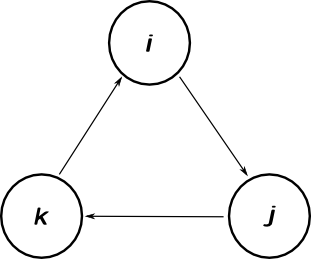
Multiplying two different imaginary units gives the positive next one in the diagram, if the arrow goes in the right way between them and negative otherwise. For example $ij=+k$, because arrow between $i$ and $j$ goes the right way. Same way $ji=-k$, $ki=j$ and so on.

Quaternions with real part zero ($q=0+ai+bj+ck$) are called pure imaginary quaternions and they have some properties that make them behave like three dimensional vectors.

Multiplication of two pure imaginary quaternions $p$ and $q$ is:

$ p\times q = (p_1i+p_2j+p_3k)\times(q_1i+q_2j+q_3k) $

$\phantom{p\times q}= -p_1q_1-p_2q_2-p_3q_3+p_1q_2k-p_1q_3j-p_2q_1k+p_2q_3i+p_3q_1j-p_3q_2i $

$\phantom{p\times q}= -(p_1q_1+p_2q_2+p_3q_3)+(p_2q_3-p_3q_2)i+(p_3q_1-p_1q_3)j+(p_1q_2-p_2q_1)k$

If we now think that quaternions $p$ and $q$ were three dimensional vectors $\vec{p}$ and $\vec{q}$, this product can be written shorter with vector calculus operators.

$\vec{p}\vec{q}= - \vec{p}\cdot \vec{q}+\vec{p}\times \vec{q}$

Where $\vec{p}\cdot \vec{q}$ is the dot product and $\vec{p}\times \vec{q}$ is the cross product.

If we change the quaternion multiplication rules to $i^2=j^2=k^2=0$, quaternion multiplication gives only the cross product. This rule and the diagram above also might help in remembering how to calculate cross product and curl without using the determinant rule.

Maxwell originally wrote his famous equations in quaternion form and they were only later rewritten in the modern vector notation. Quaternion vector calculus can do pretty much everything that the modern vector calculus can do, except the notation is little more cumbersome. For example Maxwell wrote the curl of vector v, $\nabla \times \vec{v}$, as $V\nabla v$. Where $V$ meant the vector part, $v$ is a pure imaginary quaternion and $\nabla$ is the pure imaginary quaternion similar to vector calculus $\nabla$:

$$\nabla = \frac{d}{dx}i+\frac{d}{dy}j+\frac{d}{dz}k$$

Note that $\nabla^2 = -(\frac{d^2}{d^2x}+\frac{d^2}{d^2y}+\frac{d^2}{d^2z})$, negative of the usual $\nabla^2$ in the modern vector calculus.

Even today the $i,j$ and $k$ from quaternions are sometimes used in the vector calculus as basis vectors and sometimes they can be thought to be quaternion basis units.

If you are interested in the old stuff, Maxwell's original paper "A treatise on electricity and magnetism(1873)" with quaternion notation is available at archive.org.