I was never good with remembering if derivate of $\sin x$ was plus or minus $\cos x$. Or if the derivative of $\cos x$ was plus or minus $\sin x$. I could just remember that one derivative had minus and other didn't. But I don't have that problem anymore because I can remember it now by thinking of sinc function. Limit of $\frac{\sin x}{x}$ when $x$ approaches 0 is 1, this is usually calculated using L'Hospital's rule and it can be used to remember the sign of the derivative. Using L'Hospitals rule by taking derivative of the numerator and denominator and setting x equals zero must give result of 1.

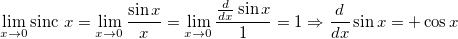
If you also remember that one of the derivatives was positive and the other was negative then because the derivative of $\sin x$ was $+\cos x$ derivative of $\cos x$ must be $-\sin x$.

I know it's a convoluted way to remember the signs of the derivatives but it works. I hope it will be useful to you too.