The other day I was coding an FPGA design that needed a source of normally
distributed random numbers. Uniformly distributed random numbers are
fairly easy and cheap to generate with a linear feedback shift register, but generating normally distributed numbers
is a harder problem. There are several ways to generate a normally distributed number
using one or more uniformly distributed, some are more accurate than others.
For my purposes the numbers don't need to exactly follow the normal distribution,,
it's enough if it seems like for a normal human that the numbers are from the normal distribution.
So I went for the easiest and cheapest implementation and use the central limit theorem, which says that summing sufficiently many
independent random numbers result will be approximately normally distributed.
I went for the sum of four uniformly distributed random numbers generated by a
linear feedback shift register. To avoid obvious period in the output I decided
to have a rather large 31-bit registers. 31-bits because it's big enough and
it needs only two taps when a 32-bit register would need four.
Code for the linear feedback shift registers:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
entity random_uniform is
generic ( SEED : STD_LOGIC_VECTOR(30 downto 0):= (others => '0');
OUT_WIDTH : integer := 11);
Port ( clk : in STD_LOGIC;
random : out STD_LOGIC_VECTOR (OUT_WIDTH-1 downto 0);
reset : in STD_LOGIC);
end random_uniform;
architecture Behavioral of random_uniform is
signal rand : std_logic_vector(30 downto 0) := SEED;
signal feedback : std_logic;
begin
feedback <= not((rand(0) xor rand(3)));
process(clk,reset)
begin
if reset = '1' then
rand <= SEED;
elsif rising_edge(clk) then
rand <= feedback&rand(30 downto 1);
end if;
end process;
random <= rand(OUT_WIDTH-1 downto 0);
end Behavioral;
|
Implementation of the linear feedback shift registers is very straight forward.
Seed value and output width can be set with generics making it also useful in many
other places.
Summing four of these uniform random numbers should generate number that is almost
normally distributed. Code for the normally distributed pseudorandom generator is
below, it outputs 12-bit signed numbers every three clock cycles, but it should
be easy to modify it to work in one clock cycle just by adding more adders.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135 | library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.NUMERIC_STD.ALL;
entity random_gaussian is
Port ( clk : in STD_LOGIC;
reset : in STD_LOGIC;
random : out STD_LOGIC_VECTOR (11 downto 0));
end random_gaussian;
architecture Behavioral of random_gaussian is
component random_uniform is
generic ( SEED : STD_LOGIC_VECTOR(30 downto 0);
OUT_WIDTH : integer);
port(
clk : in STD_LOGIC;
random : out STD_LOGIC_VECTOR (OUT_WIDTH-1 downto 0);
reset : in STD_LOGIC);
end component;
component adder_signed is
Port ( clk : in STD_LOGIC;
a : in STD_LOGIC_VECTOR (11 downto 0);
b : in STD_LOGIC_VECTOR (11 downto 0);
r : out STD_LOGIC_VECTOR (11 downto 0));
end component;
signal uniform1 : std_logic_vector(9 downto 0);
signal uniform2 : std_logic_vector(9 downto 0);
signal uniform3 : std_logic_vector(9 downto 0);
signal uniform4 : std_logic_vector(9 downto 0);
signal adder_a : std_logic_vector(11 downto 0);
signal adder_b : std_logic_vector(11 downto 0);
signal adder_r : std_logic_vector(11 downto 0);
type statetype is (s0, s1, s2);
signal state, next_state: statetype := s0;
begin
unif1: random_uniform
generic map (SEED => std_logic_vector(to_unsigned(697757461,31)),
OUT_WIDTH => 10)
port map(
clk => clk,
random => uniform1,
reset => reset
);
unif2: random_uniform
generic map (SEED => std_logic_vector(to_unsigned(1885540239,31)),
OUT_WIDTH => 10)
port map(
clk => clk,
random => uniform2,
reset => reset
);
unif3: random_uniform
generic map (SEED => std_logic_vector(to_unsigned(1505946904,31)),
OUT_WIDTH => 10)
port map(
clk => clk,
random => uniform3,
reset => reset
);
unif4: random_uniform
generic map (SEED => std_logic_vector(to_unsigned(2693445,31)),
OUT_WIDTH => 10)
port map(
clk => clk,
random => uniform4,
reset => reset
);
adder1 : adder_signed
PORT MAP (
a => adder_a,
b => adder_b,
clk => clk,
r => adder_r
);
process(clk, reset)
begin
if rising_edge(clk) then
if reset = '1' then
state <= s0;
random <= (others => '0');
else
if state = s0 then
random <= adder_r;
end if;
state <= next_state;
end if;
end if;
end process;
process(clk,state,uniform1,uniform2,uniform3,uniform4,adder_r)
begin
case state is
when s0 =>
-- Sign extend
adder_a <= uniform1(9)&uniform1(9)&uniform1(9)&uniform1(8 downto 0);
adder_b <= uniform2(9)&uniform2(9)&uniform2(9)&uniform2(8 downto 0);
next_state <= s1;
when s1 =>
adder_a <= adder_r;
adder_b <= uniform3(9)&uniform3(9)&uniform3(9)&uniform3(8 downto 0);
next_state <= s2;
when s2 =>
adder_a <= adder_r;
adder_b <= uniform4(9)&uniform4(9)&uniform4(9)&uniform4(8 downto 0);
next_state <= s0;
end case;
end process;
end Behavioral;
|
And the code of the adder for adding two 12-bit signed numbers, it has a
latency of one cycle:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.NUMERIC_STD.ALL;
entity adder_signed is
Port ( clk : in STD_LOGIC;
a : in STD_LOGIC_VECTOR (11 downto 0);
b : in STD_LOGIC_VECTOR (11 downto 0);
r : out STD_LOGIC_VECTOR (11 downto 0));
end adder_signed;
architecture Behavioral of adder_signed is
signal r_next : std_logic_vector(11 downto 0) := (others => '0');
begin
process(clk)
begin
if rising_edge(clk) then
r <= r_next;
r_next <= std_logic_vector(signed(a)+signed(b));
end if;
end process;
end Behavioral;
|
I wrote a testbench to write output values to a file and a mathematica notebook
to test how close the numbers are to the normal distribution. Histograms were generated
with "Histogram[x, 200]" command and plots with "ListPlot[x, Joined->True]", where
"x" is a list of values.
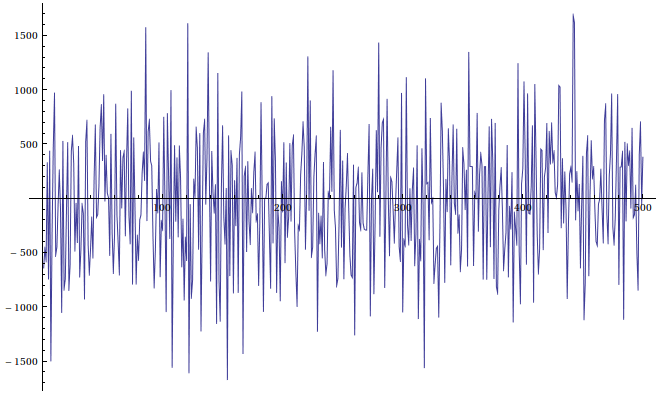
500 output values of the generator.
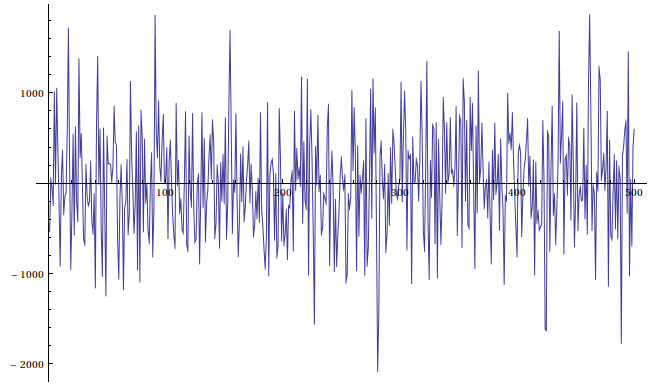
Same amount of samples from the normal distribution.
You can see that the approximation is pretty close to the normal distribution.
It's maybe a little bit fatter, but it wouldn't be noticeable without comparing
it to a true normal distribution.
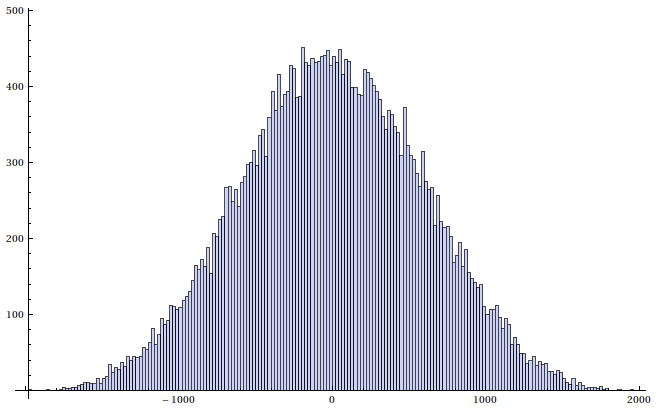
Histogram of the generated numbers. Does it look
like a normal distribution?
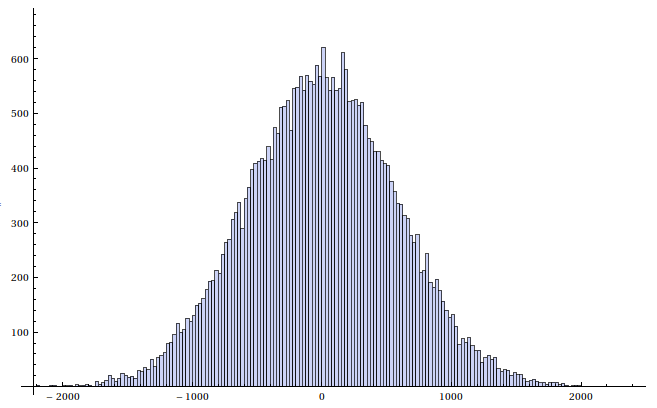
Histogram of the same amount of random numbers
generated from the normal distribution. Notice the different values on the axes.
As you can see from the histograms the approximation is a little bit flatter,
but it comes amazingly close. Just by looking at the histogram without a
normal distribution to compare it to, I would say that it is a normal distribution
and that's the only thing that was important.
Appendix 1.
VHDL test bench for writing the output values into a file:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74 | LIBRARY ieee;
USE ieee.std_logic_1164.ALL;
use std.textio.all;
use ieee.std_logic_textio.all;
USE ieee.numeric_std.ALL;
ENTITY random_gaussian_test_bench IS
END random_gaussian_test_bench;
ARCHITECTURE behavior OF random_gaussian_test_bench IS
FILE test_out_data: TEXT open WRITE_MODE is "output/gaussian.txt";
-- Component Declaration for the Unit Under Test (UUT)
COMPONENT random_gaussian
PORT(
clk : IN std_logic;
reset : IN std_logic;
random : OUT std_logic_vector(11 downto 0)
);
END COMPONENT;
--Inputs
signal clk : std_logic := '0';
signal reset : std_logic := '0';
--Outputs
signal random : std_logic_vector(11 downto 0);
-- Clock period definitions
constant clk_period : time := 10 ns;
BEGIN
-- Instantiate the Unit Under Test (UUT)
uut: random_gaussian PORT MAP (
clk => clk,
reset => reset,
random => random
);
-- Clock process definitions
clk_process :process
begin
clk <= '0';
wait for clk_period/2;
clk <= '1';
wait for clk_period/2;
end process;
-- Stimulus process
stim_proc: process
variable L1 : LINE;
variable I : integer;
begin
reset <= '1';
wait for clk_period*20;
reset <= '0';
wait for clk_period*30;
for I in 0 to 1000000 loop
wait for clk_period*3;
write(L1, to_integer(signed(random)));
writeline(test_out_data, L1);
end loop;
wait;
end process;
END;
|



