A long time ago I read from some book, probably some of the Jim William's or Bob Pease's books, interesting trick to approximate the cutoff frequency of a simple low or high pass filter. Below is equation for the cutoff frequency of a first order low or high pass filter.
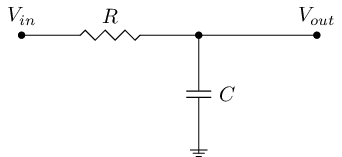
Fig 1: A simple first order low pass filter
A cutoff frequency of a filter is defined as the frequency where output power is half of output power in the pass band or equivalently the frequency where output voltage is \(1/\sqrt{2} = 0.707\). Equation for the cut off frequency of first order low or high pass filter is in Fig 2.
Fig 2: Cutoff frequency of the first order low or high pass filter
\(\frac{1}{2\pi}\) term is hard for quick calculation and it's easier to approximate it and write it in the decimal form.
This isn't still very easy to use because one farad is a too big unit in practice. We can just multiply the expression by one million and let C's unit be microfarads instead of farads. So the final approximated equation for the cutoff frequency can be written as:
Where C is in microfarads and R in ohms or C in nanofarads and R in kiloohms or any other order of magnitude as long as product of the units is 1 per one million.
This equation can be used to quickly approximate the cutoff frequency of a filter because it's easy to remember and calculate in your head. I've found it very useful myself because it provides some very much needed intuition in electrical engineering and first order filters are everywhere in analog circuits because they consist of only one capacitor and resistor.