I have been writing a sparse matrix library for few weeks and for it I needed a
algorithm for converting from coordinate list form(COO) matrix to compressed sparse column form(CSC). All of the algorithms that I found allocated space for the CSC matrix and freed the COO matrix after building the CSC matrix. This is inefficient when I know that I don't need the coordinate list matrix after building the CSC matrix. So I decided to make an algorithm that can convert the matrix in-place.
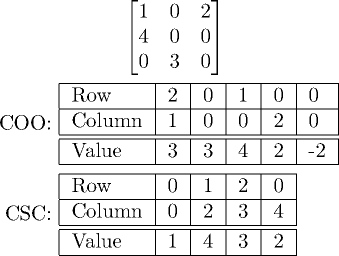
Same matrix in COO and CSC formats. COO formats order is arbitrary. This time the Column array in CSC is the same length as number of non-zero entries, but in general its length is columns in matrix + 1, or one less if you leave the last optional element out.
Above is example of same matrix in COO and CSC formats. Note that order in COO format is arbitrary and
it can have duplicate elements. Traditionally values of the duplicate entries are summed together, because this
If you look at the above CSC and COO formats of the example matrix, it should be
clear that CSC formats Value and Row arrays are just sorted COO formats Row and Value arrays. Only
problem is the Column array but it can be built easily from the sorted Column array. We just need to compare current element to previous element and if they are not equal set the next unset element to be the current loop iteration.
| Matrix->Col[0] = 0;
t = 0;
p = 1;
for(i = 1; i < Matrix->Entries; i++) {
t1 = Matrix->Col[i];
if (Matrix->Col[i]!=t)
Matrix->Col[p++]=i;
t = t1;
}
Matrix->Col[p] = i;
|
Because we want to sort the arrays in-place first choice for the sorting algorithm is Quicksort.
I know that it really requires O(log n) of space in the stack because of the recursion, but
in reality it's less than 1kB even for a several gigabyte big matrices so we don't really need to
worry about it. We need to sort both Row and Col arrays, such that Row is sorted first and then Col, but there is no need to make two passes as we can just define our comparison such that the Quicksort algorithm sorts both arrays at the same time. Below is the full algorithm and the same example matrix as above.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133 | #include <stdio.h>
#define comp(_a,_b,_x,_p) (_a[_x]!=_a[_p] ? _a[_x]-_a[_p] : _b[_x]-_b[_p])
typedef struct matrix {
int *Row;
int *Col;
double *Elements;
int Entries;
} matrix;
void COOtoCSC(matrix*);
static void q_sort(matrix *Matrix, int lo, int hi);
void COOtoCSC(matrix *Matrix) {
int i, t1, t, p, k;
/* Sort by first Col and then Row */
q_sort(Matrix, 0, Matrix->Entries-1);
k = 0;
/* Remove duplicates */
for( i = 1; i < Matrix->Entries; i++) {
if ( (Matrix->Row[k] != Matrix->Row[i]) || (Matrix->Col[k] != Matrix->Col[i]) ){
k++;
Matrix->Row[k] = Matrix->Row[i];
Matrix->Col[k] = Matrix->Col[i];
Matrix->Elements[k] = Matrix->Elements[i];
} else {
Matrix->Elements[k] += Matrix->Elements[i];
}
}
Matrix->Entries = k+1;
Matrix->Col[0] = 0;
t = 0;
p = 1;
/* Build CSC column pointers in the Col array */
for(i = 1; i < Matrix->Entries; i++) {
t1 = Matrix->Col[i];
if (Matrix->Col[i]!=t)
Matrix->Col[p++]=i;
t = t1;
}
Matrix->Col[p] = i;
return;
}
static void q_sort(matrix *Matrix, int lo, int hi ) {
int h, l, p, p1, p2, t;
double p3, td;
if(lo>=hi)
return;
l = lo;
h = hi;
p = hi;;
p1 = Matrix->Col[p];
p2 = Matrix->Row[p];
p3 = Matrix->Elements[p];
do {
while ((l < h) && (comp(Matrix->Col,Matrix->Row,l,p)<=0))
l = l+1;
while ((h > l) && (comp(Matrix->Col,Matrix->Row,h,p)>=0))
h = h-1;
if (l < h) {
t = Matrix->Col[l];
Matrix->Col[l] = Matrix->Col[h];
Matrix->Col[h] = t;
t = Matrix->Row[l];
Matrix->Row[l] = Matrix->Row[h];
Matrix->Row[h] = t;
td = Matrix->Elements[l];
Matrix->Elements[l] = Matrix->Elements[h];
Matrix->Elements[h] = td;
}
} while (l < h);
Matrix->Col[p] = Matrix->Col[l];
Matrix->Col[l] = p1;
Matrix->Row[p] = Matrix->Row[l];
Matrix->Row[l] = p2;
Matrix->Elements[p] = Matrix->Elements[l];
Matrix->Elements[l] = p3;
/* Sort smaller array first for less stack usage */
if (l-lo<hi-l) {
q_sort( Matrix, lo, l-1 );
q_sort( Matrix, l+1, hi );
} else {
q_sort( Matrix, l+1, hi );
q_sort( Matrix, lo, l-1 );
}
}
int main(void) {
int i;
int Row[] = {2, 0, 1, 0, 0};
int Col[] = {1, 0, 0, 2, 0};
double Elements[] = {3, 3, 4, 2, -2};
matrix Matrix = {0};
Matrix.Row = Row;
Matrix.Col= Col;
Matrix.Elements= Elements;
Matrix.Entries = 5;
COOtoCSC(&Matrix);
printf("Entries:%d\n",Matrix.Entries);
printf("Row:\n");
for(i=0;i<Matrix.Entries;i++) {
printf("%d\n",Matrix.Row[i]);
}
printf("Col:\n");
for(i=0;i<Matrix.Entries;i++) {
printf("%d\n",Matrix.Col[i]);
}
printf("Elements:\n");
for(i=0;i<Matrix.Entries;i++) {
printf("%f\n",Matrix.Elements[i]);
}
return 0;
}
|
Output is as expected:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | Entries:4
Row:
0
1
2
0
Col:
0
2
3
4
Elements:
1.000000
4.000000
3.000000
2.000000
|
This algorithm is fast enough for me but if you want to optimize it take a look at the glibc's qsort, which is very efficient Quicksort implementation.