Introduction

Radar can measure distance, amplitude and phase of the reflected signal. Distance to the target is usually the most important information. For a single measurement phase is not very useful as it wraps around every half wavelength distance to the target. However, with multiple measurements the change in the phase can give valuable information. Radar imaging, both synthetic and real aperture, relies on the phase information for the image formation. From the small phase differences at different locations it's possible to determine the angular location of the target.

By observing the phase of multiple consecutive measurements, very small distance changes can be measured. For example, with 6 GHz frequency the wavelength is 50 millimeters. Since the radar signal travels from radar to the target and back, a change in the distance of half the wavelength is enough to cause the distance traveled by the signal to be full wavelength. If over multiple measurements the phase changes 360 degrees, we can then determine that the distance between radar and target has changed by half wavelength, 25 mm with 6 GHz radar. For one millimeter accuracy we need to be able to measure a phase difference of 14 degrees. This seems very doable accuracy, but what's the limit?

Radar phase measurement accuracy

Let's consider a radar transmitting a linear frequency sweep. It is processed such that the result is an array of complex numbers representing the amplitude and phase of reflections from targets in that range bin. Range bin size is the range resolution of the radar. The amount of noise in one range bin depends on the minimum separable frequency resolution. This frequency resolution comes from the FFT resolution, which is one over the measurement time: $\Delta f = 1/t_s$.

We are interested in the phase measurement accuracy of signal from one target in one range bin. In that range bin we have ideal noiseless signal from the target and some amount of noise that limits the phase measurement accuracy.

If the signal-to-noise ratio of the target is $S$ then we can normalize by the signal and say that the signal is equal to 1 and noise is from complex normal distribution with mean of zero and standard deviation of $\frac{1}{\sqrt{2}S}$ for both real and imaginary components with zero covariance.

Then the question in mathematical terms becomes: what is the standard deviation of the phase of $1+ \epsilon$, where $\epsilon$ is a sample from the complex normal distribution.

Phase of a complex number $z$ can be calculated as $\text{Arg}(z) = \arctan\left(\frac{y}{x}\right)$, where $x$ is real part of $z$ and $y$ is the imaginary part.

$$\text{Arg}(1 + \epsilon) = \text{Arg}(1 + \mathcal{N}(0, \sigma) + j\mathcal{N}(0, \sigma)) = \arctan\left(\frac{\mathcal{N}(0, \sigma)}{1 + \mathcal{N}(0, \sigma)}\right) \approx \mathcal{N}(0, \sigma)$$

The above formula assumes that SNR is large so that $\mathcal{N}(0, \sigma) \ll 1$. Simplification also uses the fact that for small arguments $\arctan(x) \approx x$.

Using the relation of noise standard deviation to signal-to-noise ratio, the result is that the standard deviation of the phase measurement is $\sigma = \frac{1}{\sqrt{2}S}$, where $S$ is the signal-to-noise ratio.

Maximum SNR

Typically, at low signal strength thermal noise of the receiver is limiting the signal-to-noise ratio. At very high signal level this might not be the case. Any non-linearity, for example, from amplifier or ADC compressing, will generate mixing products. Stability of the clocks is also another limiting factor, all real oscillators output frequency drifts slightly.

Using only the radar itself, it's possible to check if thermal noise or other sources are limiting the SNR by pointing the radar at a large target (ceiling in this case) and checking if the noise level at distances where there aren't any targets changes as antennas are covered. If the phase noise is larger than thermal noise then a large target's phase noise raises noise level also at other distances. This doesn't directly tell about the SNR of the phase measurement, since in that case we care about the noise at the same distance the target is while in this measurement we compare signal strength to noise at different distance.

I set the radar to sweep from 5.4 GHz to 6.0 GHz in 1 ms. The target is a ceiling 2.5 m away (including the cable lengths to the antennas). I added attenuators to the TX output to limit RX from saturating. IF sampling frequency was 500 kHz.

In the above video the radar IF output spectrum is plotted while I cover the antennas. X-axis is distance in meters and Y-axis is amplitude in decibels (arbitrary reference). At the beginning the target amplitude at 2.5 m is about 58 dB while the noise floor at higher frequencies/distances is at around -20 dB. When the TX antenna is covered the received signal strength drops and amplitude of the target decreases by about 30 dB. Noise floor also drops by 10 dB.

-30 dB level is the thermal noise floor and as the reflected signal strength increases some other noise source raises the noise floor. It's unclear what exactly is the source of the noise. Phase noise should be about 10 dB better than this according to simulations, but with sweeping PLL it can be higher than in steady state since phase locked loop is not stabilized. Some non-linearity could also be the cause since received power is quite large.

For the phase noise measurement accuracy, it's important to know that the maximum SNR that can be measured with this radar is about 75 dB with these parameters. Calculating the SNR from variance of the noise in the largest bin also gives similar results.

Measurements

Radar and horn antennas.

Using my homemade FMCW radar I setup it up to measure its phase measurement accuracy in the best possible condition. By pointing the antennas at the ceiling, the received signal strength is maximized resulting in the best possible SNR. Ceiling is also a stable target so that its possible to assume that all the variance in the measurements are caused by the measurement setup. To avoid saturating the receiver I had to add attenuators at the transmitter output.

Rather than increasing the sweep length, SNR can be also improved by averaging multiple measurements. Making measurements faster also has advantage of being able to detect faster changes.

Frequency was swept linearly from 5.4 GHz to 6.0 GHz. The maximum sweep rate is limited by the phase locked loop sweep rate to about 32 µs at this bandwidth. I set the sweep length to 64 µs with 32 µs delay between sweeps for total of 96 µs between measurements giving about 10 kHz measurement frequency.

The phase measurement works by sending one frequency sweep which is mixed against the transmitted sweep in the receiver. The resulting signal is sine wave with frequency depending on the distance to the target. Normally in FMCW radar Fourier transform would be used to get amplitudes of reflections from each distance, but in this case where we are only looking at one distance we can instead calculate only one bin of the FFT. The phase of the resulting complex number is the wanted result.

In the video above you can see the effect of moving the antennas on the measured phase. At the start is some sinusoidal looking noise with small amplitude due to measurement setup not being completely stable. Below is the picture of the measurement with consistent scale. The noise level is not visible at full scale.

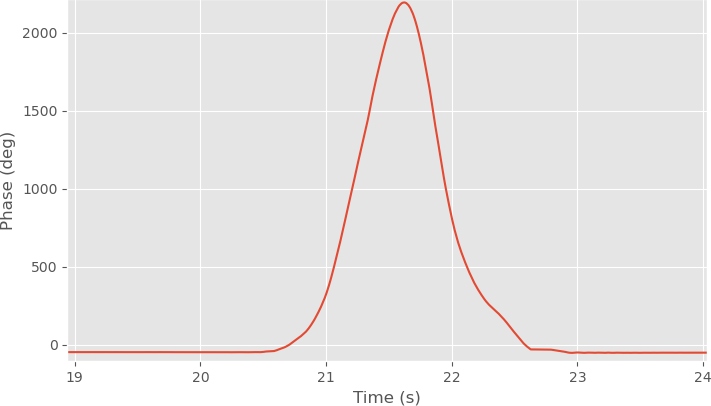
Antenna movement measurement.

Phase accuracy

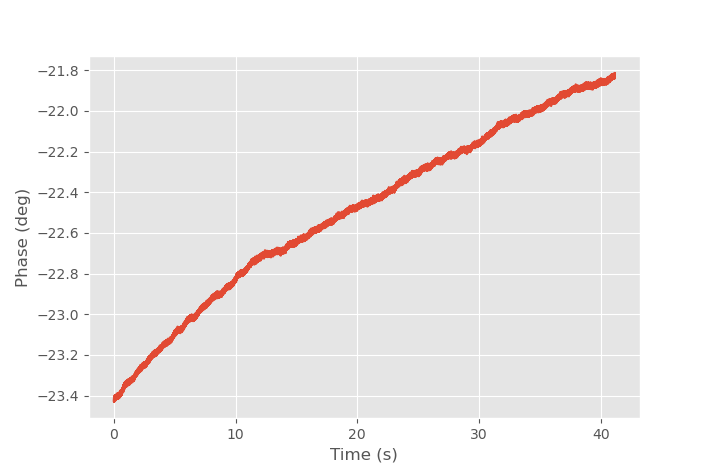
Radar pointing at ceiling.

Keeping the radar stationary pointing at the ceiling should result in a constant phase with small amount of noise. However, in the above plot there is clearly drift in the measured phase. During the 40 s measurement the phase drifted 1.6 degrees corresponding to distance change of 116 µm. The drift is caused mainly by temperature change, but also by oscillator frequency and supply voltages drifting. If the signal would be constant with white noise, it would be possible to average measurements indefinitely to obtain better accuracy. The drift makes that impossible and after some amount of averaging, the accuracy starts to get worse as the number of averages is increased.

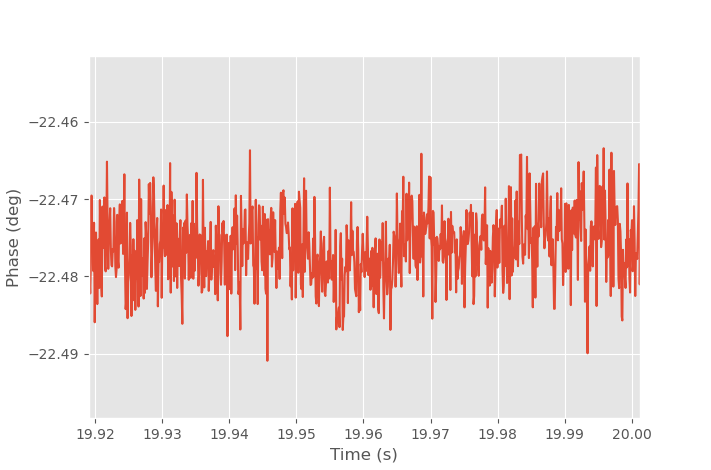
Radar pointing at ceiling, short timescale.

On the short timescale the drift is so small that the white noise from limited SNR dominates the error.

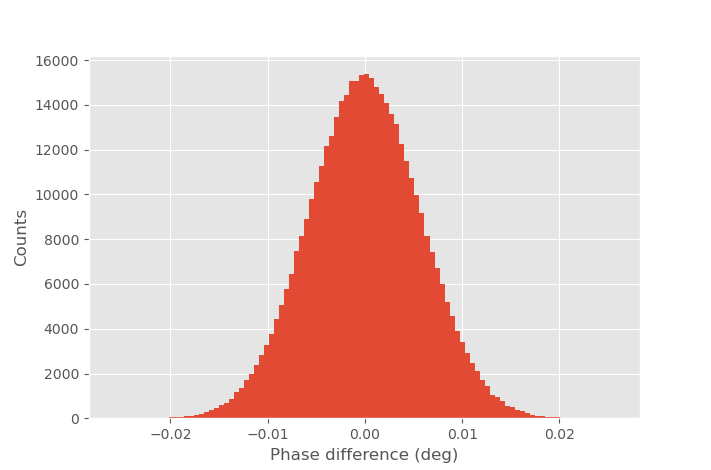
Phase difference between two successive measurements.

Plotting the phase difference between two successive measurements gives very nice looking Gaussian distribution. The standard deviation is 0.00575 degrees. Since standard deviation of difference of two normally distributed variables from the same distribution is $\sqrt{2}$ times higher than single measurement we can calculate that standard deviation of phase in single measurement is 0.0041 degrees. This corresponds to SNR of 80.0 dB.

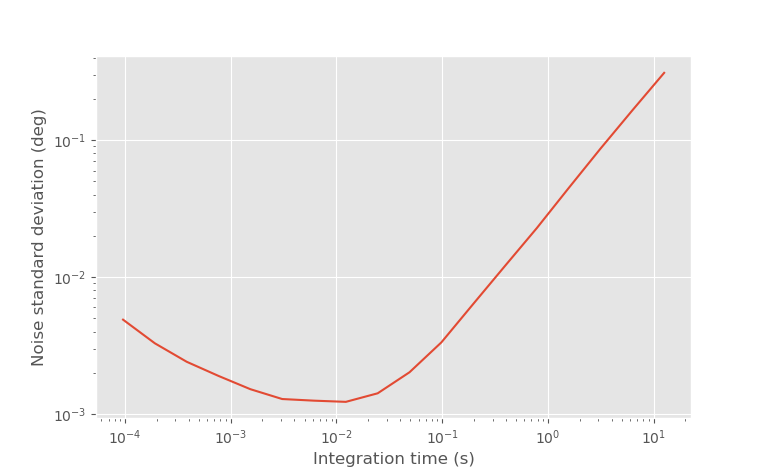
Allan deviation of phase.

The optimal averaging time can be calculated with Allan deviation. It's most commonly used for clock stability measurements, but in RF electronics it's also used to characterize radiometer accuracy with different integration times. In the above plot is the Allan deviation of the phase measurement. X-axis the integration time and Y-axis gives the standard deviation of noise at that integration time. At low integration times the white noise dominates and averaging measurements increases the measurement accuracy. At high integration times drift starts to dominate and accuracy gets worse. The optimal integration time is around 5 milliseconds (50 measurements), which should give standard deviation of 0.0012 degrees corresponding to distance of 87 nanometers. Difference of two measurements would have error $\sqrt{2}$ times larger of 0.0017 degrees corresponding to distance of 123 nm.

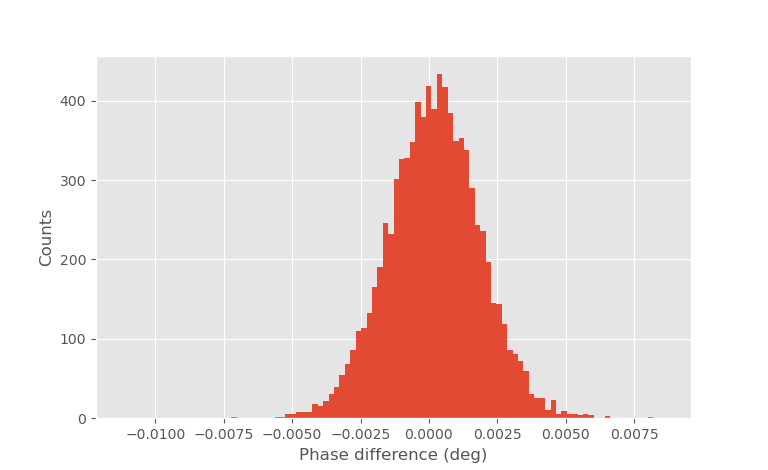
Phase difference between two successive measurements. 50 averages / measurement.

Plotting the histogram of phase difference between consecutive averages of 50 measurements gives the above plot. The calculated standard deviation is 0.0017 degrees as was predicted from the Allan deviation plot.

Light bulb vibration

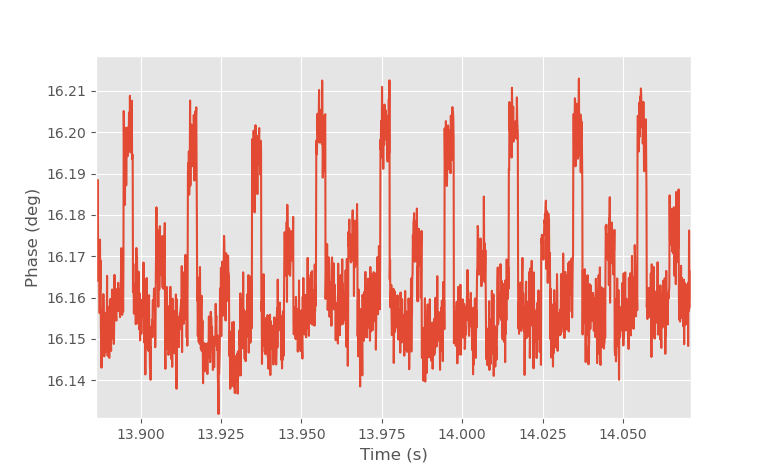
Phase measurement of radar pointing to ceiling with nearby light bulb on.

While doing the radar measurements I had an issue of extremely small but consistent frequencies in the IF signal. First I thought that it was caused by some timing issue in the radar hardware. For example, a slip of one clock cycle between ADC and PLL sweep starts could cause a phase shift in the recorded signal. However the phase shift was only about 0.04 degrees which is way below what one clock cycle error should be able to cause. After some troubleshooting I found out that turning the lights off would cause the signal to disappear. It turns out that when I pointed the antennas to the ceiling a light bulb was slightly in the antenna beam and the light bulb vibrates extremely slightly with few micrometer displacement due to mains voltage and this small movement is large enough to be detected by the radar. Any other small movements such as just being close to the radar are also highly visible in the phase plot.

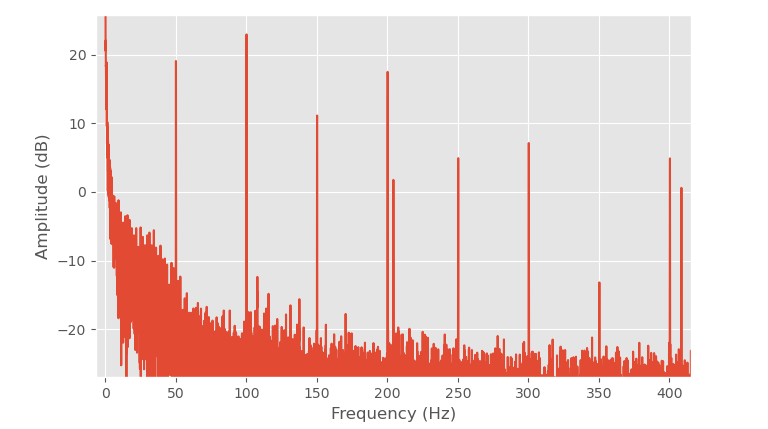
FFT of the light bulb measurement.

Taking the Fourier transform of the measurement shows that there are a lot of 50 Hz harmonics which is the grid frequency here.

Conclusion

Radar is commonly known for measuring distance to targets with quite coarse resolution, but using the phase information it can also measure chance in distance extremely accurately. By observing the phase chance of consecutive measurements, movements smaller than 1 µm can be detected in the best case. Phase change can be used to measure small vibrations such as human heartbeat and breathing rate.